提示

第六节 用数值计算法求解均匀带电圆环 、圆弧柱面和平行板的电场

在大学物理中，有限长直线均匀带电体的电场是一个十分重要的基础解，利用它的解析解可以处理一批重要的问题，如均匀带电圆环、圆弧柱面和平行板的电场等。

首先给出有限长直线均匀带电体的电场：由库仑定律知，线电荷密度为λ、长度为dl的带电线元的电场为

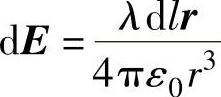
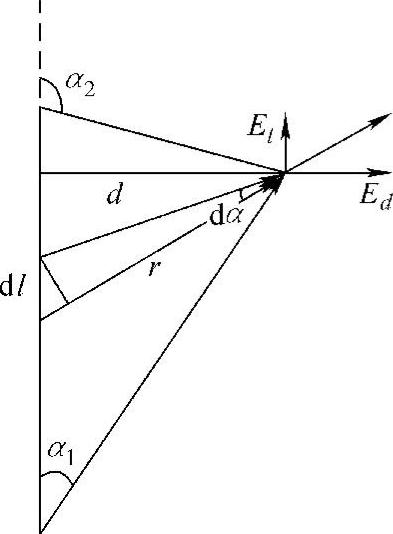
图2-6-1 有限长直线均匀带电体的电场

利用关系dlsinα=rdα（见图2-6-1）不难得到在过带电线平面空间r处的电场，可将其分解为平行于带电线方向和垂直于带电线方向的两个分量：

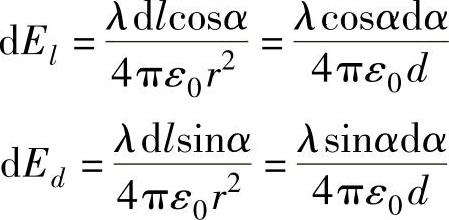
所以

图2-6-2 均匀带电圆环的电场

从以上公式出发，我们可以利用数值计算法解决均匀带电圆环、圆弧柱面和平行板的电场。

均匀带电圆环的电场

求解思路：从圆内接正2n边形带电线的电场过渡到均匀带电圆环的电场，即用圆内接正多边形带电线的电场的解析解去逼近带电圆环的电场的解析解。

（1）数学建模 如图2-6-2所示，圆半径：R，矢量R_i（i=0→n），且R_i=（x_i=Rcosa_i，y_i=Rsina_i，z_i=0）其中，

边长：l_n，矢量l_i，i+1（i=0→n-1），且

正多边形的顶点到考察点的矢径：r_i=（x-x_i，y-y_i，z）

其大小为

边长与矢径的夹角及夹角余弦：

电场的方向E_il//l_i，方向余弦

其中，，

最后不难得到

（2）三个子程序和一个主程序

1）绘制多边形线圈

2）计算单个线圈电场的值

3）获得多个圆环电场矢量的值

4）主程序

下面是用《科学计算与模拟平台》绘制的均匀带电圆环的电场矢量表示图及场线表示图（图2-6-3、图2-6-4）。

图2-6-3 均匀带电圆环的电场（矢量表示）

图2-6-4 均匀带电圆环的电场（场线表示）

由数学上的线动成面的思想，利用有限长带电线电场的解析解可求均匀带电圆弧柱面的电场和平行板电容器的电场的数值解。

练习2-6-1 求均匀带电圆弧柱面的电场（图2-6-5）。

练习2-6-2 求有限大平行板电容器的电场（图2-6-6）。

图2-6-5 均匀带电圆弧柱面的电场

图2-6-6 有限大平行板电容器的电场